| john@email.johncon.com |
| http://www.johncon.com/john/ |
|
|
|
||
Stochastic UCE Detection |
|||
Home | John | Connie | Publications | Software | Correspondence | NtropiX | NdustriX | NformatiX | NdeX | Thanks
|
A cute application of information theory-a 64 line procmail(1) script fragment that can be used to filter spam, (e.g., Unsolicited Commercial E-mail, UCE, or bulk e-mail.) The fragment can be included in a user's ~/.procmailrc, or system wide /etc/procmailrc files, and establishes a cumulative score of the probability that a specific message is spam. The cumulative spam score consists of scores for header construction, (primarily determined by whether the message was transmitted through open relay, or ISP dial up,) and body content, (primarily determined by the message having an opt-out clause.) If the message's cumulative spam score is sufficiently high, the message is filed in the user's "spam" mail box folder, (which could be /dev/null.) If sufficiently low, the message is filed in the user's mail box folder, and in between, in the user's "junk" mail box folder. The advantage of the scheme is that the disposition of a message is not dependent on any single characteristic, (for example, the message being transmitted through a black listed machine is not sufficient, in itself, to discard the message.) For analytical details, see the section on Theory, and the Results section contains performance metrics. Description and Walk Through of the Script FragmentMany of the database functions used in the fragment are available from the E-mail "Received: " Header IP Address Auditing suite-most have alternative implementations using standard procmail constructs. The variable SPAMSCORE is the cumulative spam score, and is initialized to zero; a score of zero means that there was nothing found to indicate the message is spam, a low negative score, say, smaller than -1841022, means that it is a virtual certainty that the message is not spam, and a high negative score, say, larger than -20736769, means that it is a virtual certainty that the message is spam:
SPAMSCORE="0"
Messages that have a negative cumulative spam score larger than -20736769, (corresponding to six sigma,) will be considered spam. Those larger than -1841022, (corresponding to one sigma,) will be considered junk, and less, valid. These sigma limits are conservative, and somewhat arbitrary-they can be altered to adjust false positive and disposition compromises. Save the machine generated return address of the sender using the formail(1) program that is distributed with procmail:
:0 whc
SENDER=| formail -rzx To:
Save the trusted return address of the sender-the address is extracted from the "Reply-To:" and "From:" header records:
:0 whc
FROM=| formail -rztx To:
Extract the sender's domain name from the machine generated return address of the sender-the domain name will be used in evaluation of header construction:
:0 whc
DOMAIN=| formail -rzx To: | sed 's/^.*@//'
Query the user's files, ~/.procmail.accept and ~/.mailrc, for the trusted and machine generated return address of the sender. The ~/.procmail.accept file is a Unix flat file database, (i.e., organized in lexical order, all lowercase, and made with sort -u; look(1) may be a suitable alternative to bsearchtext(1), which is available from E-mail "Received: " Header IP Address Auditing.) The file contains all e-mail addresses the user has ever received e-mail from, i.e., it is a white list; it is used to prevent valid e-mail from false positive errors in spam detection. The database can be maintained using the rel(1) full text information retrieval system at NformatiX, which is capable of extracting all addresses with a simple shell script, and converting the addresses to lower case characters:
:0
* 1^0 ? bsearchtext -r n -f "${HOME}/.procmail.accept" \
"${FROM}" "${SENDER}"
* 1^0 ? fgrep -i -s -e "${FROM}" "${HOME}/.mailrc"
{
SPAMSCORE="27384317"
}
Note that absence of either, or both, file(s), will not be of consequence-the cumulative spam score will remain zero. If the sender's address is found in either the ~/.procmail.accept or ~/.mailrc files, then the sender is known; set the cumulative spam score, SPAMSCORE, to a virtual certainty, (corresponding to 7 sigma in this case,) that the message is valid, and not spam. The following "recipe" is the main determination of the message's cumulative spam score; it evaluates the message's header construction. If a condition is true, the natural logarithm of the probability that the message is spam do to the conditional is added to the cumulative spam score:
:0
* $$SPAMSCORE^0
* -3361741^0 !^to:
* -6454846^0 ^to:.*[<] *[>]
* -6258282^0 ^to:.*undisclosed.*recipient
* -4448203^0 ^cc:.*recipient.*list.*not.*shown
* -5135798^0 ^received:.*microsoft exchange
* -2167692^0 ^received:.*microsoft smtpsvc
* -1272966^0 $ !^received:.*"${DOMAIN}
* -1257903^0 $ !^message-id:.*"${DOMAIN}
* -2217521^0 ^subject:.*!
* -10361956^0 ^x-advertisement:
* -5855766^0 ^subject:.*adv(ertise(ment)?.*)?([ .:-]|$)
* -5750007^0 ? test "${SENDER}" != "${FROM}"
* -1989573^0 !? receivedTodb -r m \
"${HOME}/.procmail.addresses"
* -5213281^0 ? receivedIPdb -r n \
"${HOME}/.procmail.reject"
* -2663031^0 ? receivedMSGIDdb -r n -f ${FROM} \
"${HOME}/.procmail.domains"
* -4563378^0 ? receivedUnknowndb -r n \
"${HOME}/.procmail.domains"
{ }
SPAMSCORE=$=
Walking through the "recipe", starting with the current cumulative spam score, SPAMSCORE:
There are several ancillary searches to the body of a message (specifically, searching for encoding and opt-out clauses,) that can yield results in spam determination:
:0
* < 1000000
{
:0 B
* $$SPAMSCORE^0
* -1409686^0 base64
* -847052^0 delete
* -4750287^0 mailing
* -2342018^0 $ ${dq}mailto:
* -2125098^0 remove
* -1468567^0 unsolicited
* -8449986^0 unsubscribe
{ }
SPAMSCORE=$=
}
Walking through the "recipe", (scan the body of the message if the message's size is less than one MB,) starting with the current cumulative spam score:
Tally the cumulative spam score: If the message's cumulative spam score is greater than an arbitrary six sigma, then file the message in the spam folder:
:0
* 20736769^0
* $$SPAMSCORE^0
{ }
#
:0 E:
spam
Else, if the message's cumulative spam score is greater than an arbitrary one sigma, then file the message in the junk folder:
:0
* 1841022^0
* $$SPAMSCORE^0
{ }
#
:0 E:
junk
Else, the message has a reasonable certainty of being a valid non-spam message; file it in the user's inbox folder.
:0:
inbox
TheoryConsider two archives of e-mail messages. The first, A, contains only spam messages, the second, B, only messages that are not spam, i.e., valid e-mail. In the first archive, A, some messages will have a given characteristic, and some will not. Likewise for the second archive, B. The probability, Pa, that a message in the first archive, A, has the characteristic is the number of messages in the A archive that have the characteristic divided by the number messages in archive A. Likewise, the probability, Pb, of a message having the characteristic in the second archive is the number of messages with the characteristic divided by the number of messages in the archive. Now assume a message, selected randomly, has the characteristic-what is the probability that it is from the A archive? The B archive? The probability, P, that the message is from the A archive is:
P = Pa / (Pa + Pb)
and from the B archive:
P = Pb / (Pa + Pb)
Some sanity tests considering a message with the characteristic, selected randomly from either archive:
Suppose the characteristic is being used to determine the chance that the message is spam. If the message is spam, the message should be classified in the A archive. If not, the B archive. Note that the chance that the message should be classified in the B archive is the probability, Pf, of a false positive, e.g., the message has the characteristic, but is not spam. The probability, Ps, that the message is spam is Pa, e.g., the message has the characteristic and is spam. So, Ps is the probability that a message is spam if it has the specific characteristic. Ps is calculated as the quotient of the number of messages in the spam archive that has the characteristic, and total number of messages in the spam archive. And, Pf is the probability that a message is not spam if it has the specific characteristic, i.e., the probability of a false positive for the characteristic. Pf is calculated as the quotient of the number of messages in the non-spam e-mail archive that have the characteristic, and the total number of messages in the non-spam archive. From information theory, (and the above intuitive arguments-its actually Bayesian Analysis, depending on one's point of view,) the probability, Pt, of a correct assessment that the message is spam is:
Pt = Ps / (Ps + Pf)
And, the probability of an incorrect assessment is:
1 - Pt = 1 - (Ps / (Ps + Pf)) = Pf / (Pf + Ps)
But for Pf << Ps, and Ps near unity, the probability of an incorrect assessment is approximately Pf, e.g., if one was to make a wager on whether a message with the characteristic is spam, or not, one would do so based on the more on the value of Pf instead of Ps. Note the significance; the probability, Ps, that a message is spam is not as important as the probability of a false positive, Pf. It is a subtle point. If there are multiple characteristics typical of spam, and the probabilities of the false positives of those characteristics are statistically independent, then the probabilities of a false positive, Pf, for each characteristic can be multiplied together to get the overall probability of a false positive in declaring the message spam. Note the scheme. All messages are assumed to be spam, and the probability of a false positive calculated-which is counter intuitive. Based on the value of the probability, the message is "bined" against the cumulative of the Normal Probability Function. For example, if a message has a total probability, do to all characteristics, of one standard deviation, i.e., one sigma, then there would be a probability of 15.9% that the message was not spam. For two standard deviations, 2.2%, and three, 0.13%, and so on. Obviously, the more characteristics, the better, and the characteristics that should be selected should have the largest Ps, while at the same time, the smallest Pf, e.g., for all characteristics, Pf << Ps. Note that the issue is that the problem is really underspecified, (see Combining Probabilities for particulars,) requiring a heuristic/engineered solution: the statistics on a very large e-mail archive, (32,000 messages in this case-giving a statistical precision of about 1 / 32,000, or about 4 sigma,) is measured, and the empirical spam limit set such that none of the legitimate e-mail messages would be rejected; anything above that limit is considered spam, and can be rejected outright. ImplementationProcmail has a conditional summation mechanism:
SCORE="0"
#
:0
* 1^0 a condition
* 2^0 a different condition
* 3^0 another different condition
{
SCORE=$=
}
where the value of the variable SCORE is zero if no conditions are true, unity if only the first, three if only the third, four if the first and third are true, and so on-its a weighted scoring technique. To use cumulative weighted scoring with probabilities, the numbers must be logarithms-since they must be multiplied together for each true conditional; summing logarithms of numbers is the same as multiplying the numbers together, (note that the sum of the logarithms of the probabilities is the same as the chi-square of a uniform distribution with n many degrees of freedom, -2 * sum ln (pn), for the probabilities, pn, without multiplying by 2.) For example, suppose that the first condition has a probability of a false positive, Pf, of 10%. The second 20%, the third 30%. The natural log of 0.1 = -2.3026, and 0.2 = -1.6094, and 0.3 = -1.2040. So the previous construct would look like:
SCORE="0"
#
:0
* -2.3026^0 a condition
* -1.6094^0 a different condition
* -1.2040^0 another different condition
{
SCORE=$=
}
which can be compared against the natural logarithm of the cumulative of the Normal Probability Function for combined false positive rates:
where the standard deviation values were computed by the sigma program. The table allows "bining" of messages by standard deviation of probability of false positive. These values-multiplied by 1000000, and truncated for integer arithmetic-were then used in the fragment script for production. As an example, suppose all three conditions in the above example construct were true; then the value of the variable SCORE would be -5.116, (or between a two and three standard deviation-actually, 2.5122-the probability of a false positive.) As a check, e^-5.116 = 0.006, which is 0.1 * 0.2 * 0.3. A 2.5122 standard deviation would represent a probability of 1 in 167 of a false positive. Historical Perspective and Implementational AsidesDetermining relevance of documents to a set of keywords, (or keyword counts in other documents,) is not new. As far as I know, the first mention of the concept was by none other than Vannevar Bush in an extension to the Memex Machine. (For details, see "From Memex to Hypertext: Vannevar Bush and the Mind's Machine," James M. Nyce, Paul Kahn, Academic Press, Inc., Boston, ISBN 0-12-523270-5, 1991, pp. 145-164, specifically, the section on page 156 titled The Statistical Machine, explored by Bush's student assistants starting in 1938-with marginal success in cryptographics through 1943.) For example, most Internet search engines work that way, as do most e-mail archive retrieval systems, (like the rel program.) However, note that, in some abstract sense, what is done in this implementation is the exact opposite-an e-mail is assumed to be spam/UCE, and combined chances of a false positive in the assumption calculated; if the combined chances of a false positive are not sufficiently small, the assumption is rescinded. Note the subtle difference-the problem is not in determination of whether a specific e-mail is spam/UCE, but whether the confidence in that determination is enough to assert a decision about it; its similar to political polls where a confidence interval around an empirical metric is used to judge the quality of an assertion. Also, this implementation does not look into the body of an e-mail message to determine relevance to spam/UCE criteria, (such as word instance counting, or probabilities.) Only the header and construction of the body is analyzed; although word instance calculations could be used, procmail(1) is probably not the preferred choice, since multiple word parsing of large documents is a computationally expensive exercise with regular expressions. (See: Paul Graham's suggestions for a better alternative.) Additionally, as another procmail(1) expediency, Bayes' Rules, (see also, Paul Graham's comments,) for conditional probabilities is approximated by using the product of the chances of the conditional false positives, Pf, which is valid if, and only if, all the conditional Pfs are much less than unity, (which is a reasonable, and conservative, approximation when working with well chosen false positive criteria, e.g., Pf << Ps and Pf << 1, which is the technique/methodology used in this implementation.) Since the technique/methodology depends on determining the combined probability of false positives as a decision criteria, it is closer to information-theoretic techniques than traditional methods of Bayes' Natural Language inference-thus the name, Stochastic UCE detection. Empirical DataThe spam statistics shown in TABLE I were derived from an e-mail archive consisting of 31,632 messages. The dates on the messages spanned July 1993, to July 2001. 1302 of the messages were spam-all from May 2001 to July 2001. The archive was divided into two archives; one containing non-spam messages, the other containing only spam. The procmail script fragment was modified:
:0: Hc
* !^to:
/home/user/no-to
#
:0: Hc
* ^to:.*[<] *[>]
/home/user/to-brackets
#
:0: Hc
* ^to:.*undisclosed.*recipient
/home/user/to-undisclosed
#
:0: Hc
* ^cc:.*recipient.*list.*not.*shown
/home/user/cc-recipient
.
.
.
and so on, for each conditional in TABLE I. The script was executed on the Email archive with the shell command:
for i in Email/*
do
procmail /home/user/fragment < $i
done
and the e-mail in the various files in /home/user created by the fragment script counted:
egrep 'From ' /home/user/no-to | wc
The fragment script was then used on the Spam directory, and the results for both the Email and Spam directories tabulated for TABLE I. The values from TABLE I-multiplied by 1000000, and truncated for integer arithmetic-were then used in the fragment script for production.
[1]Although no valid messages were found in the e-mail archive with the "^to:.*< *>" characteristic, that doesn't mean that messages do not exist with the characteristic. A conservative assumption would be that the next message in an archive of 31,632 messages would have the characteristic-message number 31,633 does. Or, a virtual certainty is one in 31,633, or a probability of 1 - 3.16125565E-5. Note the implication; If a message has a probability of 1 - 3.16125565E-5 of being spam, then it is a virtual certainty that it is spam, do to data set size limitations. [2]An "X-Advertisement:" header was proposed by the industry to identify spam messages. It never worked out, and none were found in either the spam or e-mail archive. Assume none found in the e-mail archive, some found in the spam archive, or a virtual certainty of 1 - 3.16125565E-5 based on data set size limitations. [3]For non-spam e-mail using Microsoft Exchange and IIS as the MTA, the e-mail archive consisted of 3042 messages. The dates on the messages were restricted to spanning January 1, 2000, to July 2001 to provide a representative false positive rate. Neither product was deployed in significant numbers prior to January 1, 2000. ResultsCombining the messages in the Email and Spam directories from the Empirical Data section, and consecutively executing the fragment script with procmail resulted in 72.4750277%, (or almost three forths,) of the spam messages being filed in the spam mail box folder-there were no false positives due to conservative false positive settings. Production metrics validate the statistics, and 53.164556962% of the messages from someone a user has never corresponded with before will be filed in the junk folder, with no false positives in the spam folder-there were no false positives due to conservative false positive settings. Note: the default conservative false positive settings are suggested due to small data set size-31,632 messages, of which 1,302 were spam. Small data set size increases the chances of a false positive, substantially, above predicted values. For example, a reliable false positive incident rate estimate of one in a billion, (6 sigma,) would require a data set size of over a billion messages. The fragment averages under a tenth of a second of CPU time (on a single CPU 433MHz Pentium class machine,) to deliver a message. A less conservative, more aggressive, technique, with small data set sizesAs example methodology of working with smaller data set sizes, the fragment was used on several days of e-mail and spam messages, which were archived for evaluation of the SPAMSCORE variable. There were 42 e-mail messages, (from e-mail addresses never corresponded with before, i.e., the query always returned negative,) and 93 spam messages. For e-mail, the SPAMSCORE ran between 0 and -15,325,371, and for spam, between -1,989,573 and -57,849,849. The average SPAMSCORE, using the tsavg program, for e-mail was -3,643,522.809524 and -21,478,120.290323 for spam. The root mean square of the SPAMSCORE, using the tsrms program, for e-mail was -5,347,103.873589 and -25,052,060.683733 for spam. From the tsstatest program, the average SPAMSCORE for e-mail was -3,643,522.809524, with an estimated error of 2,151,016.649996 = -59.036728%, and -21,478,120.290323 for spam, with an estimated error of 6,727,700.056786 = -31.323505%. The root mean square of the SPAMSCORE for e-mail was -5,347,103.873589 with an estimated error of 1,520,998.459658 = 28.104602%, and -25,052,060.683733, with an estimated error of 4,757,202.331943 = 18.886897% for spam. The estimated error was for a 99% confidence interval. The false positive incident rates can be computed from the root mean square values. The confidence interval adjustment to the root mean square value for e-mail is -5,347,103.873589 -1,520,998.459658 = 6,868,102.33323, and -25,052,060.683733 - 4,757,202.331943 = 29,809,263.0156 for spam. What this means is that if we repeat this evaluation on different archives of e-mail and spam many times, 99% of the time, the root mean square values will be less than 6,868,102.33323 for e-mail, and 29,809,263.0156 for spam; and 1% more. So, those are very conservative estimates on the root mean square values. A false positive rate of 4 sigma, (corresponding to 1 in 31,574.3873622,) would require a negative spam score greater than -3,643,522.809524 -2,151,016.649996 - (4 * 6,868,102.33323) = 30,034948.7924. For a 3 sigma false positive rate, (corresponding to 1 in 740.796695584,) the value would be 26,398,846.4592, (or, since the average for spam is -21,478,120.290323 -6,727,700.056786 = 28205820.3471, assuming a right tail confidence level, or a setting of between 3 and 4 sigma would have a false positive rate between 1 in 741 and 1 in 31,574, while rejecting approximately half the spam, everything greater than the average spam score, 28205820.3471.) The frequency distribution of values for SPAMSCORE for e-mail and spam is graphed in Figure I, (which is available in larger size jpeg, PostScript, or PDF formats.) The aberration in the spam frequency having a value at a SPAMSCORE greater than zero is the result of numerical stability issues-in subtracting the average from the time series for plotting with the tsnormal program. (As an aside, look at the large proportion of e-mail that had a perfect SPAMSCORE of zero-showing a great deal of craftsmanship by the e-mail system folks in the industry.) 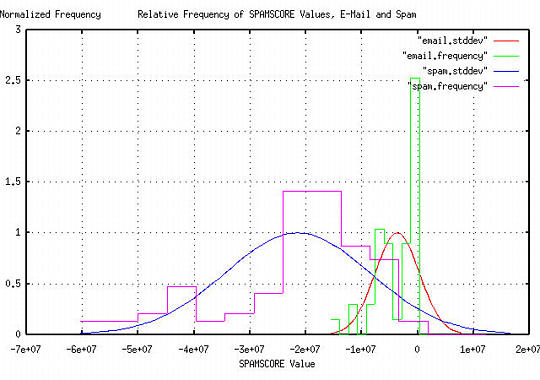 Figure I. Relative Frequency of SPAMSCORE Values, E-Mail and SpamFigure I shows that, although the numerical analysis is about right, and using a negative spam score slightly larger than the largest value found in e-mail, (-15,325,371, corresponding to a 5.06 sigma value,) would suffice, and would reject 73.1182796% of the spam archive, with no false positives in the e-mail archive. Note that the frequency distributions are skewed toward zero, (indicating that the distributions are not normal error functions,) biasing the analysis to higher values. (The numerical methods used in the analysis-particularly the statistical estimation and root mean square calculations-were predicated on a Gaussian/normal frequency distribution.) Note that this is an example methodology, and a more sophisticated approach would automate the Empirical Data collection, and numerical methods in this section-dynamically updating the variables in the fragment section in user's ~/.procmailrc file. This would require users to "bounce" spam to an e-mail archive, perhaps implemented with the rel(1) full text information retrieval system at NformatiX. The accuracy of the variables would be refined as the archive increases in size, raising the confidence level of the statistical estimate-although it is doubtful that more than 80%-90%, (about one standard deviation,) of the spam could be removed using this methodology. However, even with small data set sizes, those numbers can be approached. ExtensionsThe database programs used in the procmail fragment are from the E-mail "Received: " Header IP Address Auditing web page. Additionally, the fragment is compatible with Quarantining Malicious Outlook Attachments fragment. For maintaining e-mail and spam databases as a full text information retrieval system, the programs at NformatiX can be used. Note that the fragment is very effective at determining the likelihood of a message being from an unknown valid user, as opposed to being spam, making Certified Mail Delivery and SMTP based sender authentication a reasonable proposal. If dynamic update of database information is desired, the constant databases used in the E-mail "Received: " Header IP Address Auditing suite can be replaced with cdb from D. J. Bernstein. AddendumAs an example of adding a spam conditional to the fragment, it was observed that the Quarantining Malicious Outlook Attachments fragment performed fairly well as a spam detector. 1994 recent non-spam e-mail were placed in a directory, and 235 recent spam messages in another. The fragment was "hacked" to file the messages in one of two folders, one containing messages with potentially malicious attachments/content, and the other non-malicious. The fragment was run on both directories with a single line shell script, and it was found that 137, (137 / 235 = 0.582978723,) of the spam messages contained malicious content, vs, 265, (265 / 1994 = 0.132898696,) for the e-mail directory. The value for 1 - Pt, (from the Theory section,) would be 0.132898696 / (0.132898696 + 0.582978723) = 0.185644487. And converting to a procmail conditional value, -1,000,000 * ln (0.185644487) = 1,683,921.79603, or the procmail conditional would look like:
* -1683922^0 ? test "${MALICIOUS}" -gt "0"
where the value of $MALICIOUS is 1 if the message contains potentially malicious attachments, or -1, if it doesn't. The entire process took under 15 minutes. So, the data in TABLE II:
could be included in TABLE I, also. As another example of adding a spam conditional to the fragment, it was observed that a significant amount of spam contained URL addresses with dotted quad notation, (i.e., of the form "http://123.123.123.123".) 34105 non-spam e-mail were placed in a directory, and 901 recent spam messages in another. Both directories were searched, using "egrep -il 'http://[0-9]+\.[0-9]+\.[0-9]+\.[0-9]+'", and it was found that 174 (174 / 901 = 0.193118757,) of the spam messages contained URL addresses with dotted quad notation, vs, 87 (87 / 34105 = 2.55094561E-3,) for the e-mail directory. The value for 1 - Pt, (from the Theory section,) would be 2.55094561E-3 / (2.55094561E-3 + 0.193118757) = 1.30369985E-2. And converting to a procmail conditional value, -1,000,000 * ln (1.30369985E-2) = 4,339,963.92906, or the procmail conditional would look like:
* -4339964^0 http://[0-9]+\.[0-9]+\.[0-9]+\.[0-9]+
The entire process took under 10 minutes. So, the data in TABLE III:
could be included in TABLE I, also. As another example of adding a spam conditional to the fragment, it was observed that a significant amount of spam contained "^Content-Type: text/html" records in the header in an effort to format the message automatically. 34786 non-spam e-mail were placed in a directory, and 754 recent spam messages in another. Both directories were searched, using a short procmail script, and it was found that 373 (373 / 754 = 0.49469496,) of the spam messages contained the content header, vs, 18 (18 / 34786 = 5.17449549E-4,) for the e-mail directory. The value for 1 - Pt, (from the Theory section,) would be 5.17449549E-4 / (5.17449549E-4 + 0.49469496) = 1.04490424E-3. And converting to a procmail conditional value, -1,000,000 * ln (1.04490424E-3) = 6,863,830.03024, or the procmail conditional would look like:
* -6863830^0 ^content-type:[ ]+text/html
So, the data in TABLE IV:
could be included in TABLE I, also. Note that this conditional is not statistically independent from the above conditional:
* -1683922^0 ? test "${MALICIOUS}" -gt "0"
There is a slight interaction, (depending on whether the HTML code has extensions, or not.) As yet another example of adding a spam conditional to the fragment, it was observed that a significant amount of spam contained "opt-out" clauses in the body of the message. 35628 non-spam e-mail were placed in a directory, and 1208 recent spam messages in another. Both directories were searched, using a short egrep(1) script with [^a-z]opt-?(in|out)[^a-z] as the search argument, and it was found that 142 (142 / 1208 = 0.117549669,) of the spam messages contained the "opt-out" clause, vs, 60 (60 / 35628 = 1.68406871E-3,) for the e-mail directory. The value for 1 - Pt, (from the Theory section,) would be 1.68406871E-3 / (1.68406871E-3 + 0.117549669) = 1.41240956E-2. And converting to a procmail conditional value, -1,000,000 * ln (1.04490424E-3) = 4,259,873.03136, or the procmail conditional would look like:
* -4259873^0 [^a-z]opt-?(in|out)[^a-z]
So, the data in TABLE V:
could be included in TABLE I, also. As yet another example of adding a spam conditional to the fragment, it was observed that a significant amount of spam contained machine generated "Return-Path: header records. 4075 non-spam e-mail were placed in a directory, and 1019 recent spam messages in another. Both directories were searched for "Return-Path: " records using a short egrep(1) script with .*[-=+?].*[-=+?].*@, .*[0-9][^0-9].*@, and, [0-9][0-9][0-9][0-9][0-9][0-9].*@ as search arguments, and it was found that 22 (22 / 1019 = 2.15897939E-2,) of the spam satisfied the .*[-=+?].*[-=+?].*@ search criteria, 163 (163 / 1019 = 1.59960746E-1,) satisfied the .*[0-9][^0-9].*@ criteria, and, 47 (47 / 1019 = 4.61236506E-2,) the [0-9][0-9][0-9][0-9][0-9][0-9].*@, vs, 144 (144 / 4075 = 3.53374233E-2,) for .*[-=+?].*[-=+?].*@, 83 (83 / 4075 = 2.03680982E-2,) for .*[0-9][^0-9].*@, and, 6 (6 / 4075 = 1.47239264E-3,) for [0-9][0-9][0-9][0-9][0-9][0-9].*@. The values for 1 - Pt, (from the Theory section,) respectively, would be 6.20747422E-1, 1.12949752E-1, and, 3.093518992E-2. And converting to a procmail conditional value, respectively, -1,000,000 * ln (6.20747422E-1) = 476,831.00830, -1,000,000 * ln (1.12949752E-1) = 2,180,812.23406, and, -1,000,000 * ln (3.093518992E-2) = 3,475,860.91079, or the procmail conditional would look like:
* -476831^0 ^return-path:[ ]+.*[-=+?].*[-=+?].*@
* -2180812^0 ^return-path:[ ]+.*[0-9][^0-9].*@
* -3475861^0 ^return-path:[ ]+\
.*[0-9][0-9][0-9][0-9][0-9][0-9].*@
So, the data in TABLE VI:
could be included in TABLE I, also. Note that the conditionals are not statistically independent, and only one should be used-probably:
* -3475861^0 ^return-path:[ ]+\
.*[0-9][0-9][0-9][0-9][0-9][0-9].*@
As yet another example, the word frequencies in the bodies of 1,291 spam e-mail were compared against the frequencies in the bodies of 4,172 non-spam e-mail by modifying the source code to the rel program from the NformatiX site to find word instance frequencies in both the e-mail and spam archives. After constructing several word instance frequency databases, (structured as described in the Theory Section, above,) using modified versions of the bsearchtext program from the ReceivedIP page, the following procmail(1) script was used to evaluate the effectiveness of body word frequency counts on both the spam and e-mail archives:
:0 B
* -12272912^0
# * 8449986^0 ([^a-z]|^)unsubscribe([^a-z]|$)
* 8021776^0 ([^a-z]|^)refinance([^a-z]|$)
# * 4750287^0 ([^a-z]|^)mailings?([^a-z]|$)
* 4339964^0 http://[0-9]+\.[0-9]+\.[0-9]+\.[0-9]+
* 4259873^0 ([^a-z]|^)opt-?(in|out)([^a-z]|$)
* 3792871^0 ([^a-z]|^)advertise(ments?|ing|rs?)?([^a-z]|$)
* 3150439^0 ([^a-z]|^)unbelievable([^a-z]|$)
* 3059374^0 ([^a-z]|^)testimonials?([^a-z]|$)
* 2957743^0 ([^a-z]|^)promo(t(er?|ion(al)?|or))?([^a-z]|$)
* 2903651^0 ([^a-z]|^)remov(ed?|al)([^a-z]|$)
* 2596350^0 ([^a-z]|^)obligat(e|ion)([^a-z]|$)
* 2570780^0 ([^a-z]|^)shop(p(er|ing))?([^a-z]|$)
* 2342018^0 $ ${dq}mailto:
* 2315228^0 ([^a-z]|^)financial(ly)?([^a-z]|$)
* 2281832^0 ([^a-z]|^)solicit(ed)?([^a-z]|$)
* 2185652^0 ([^a-z]|^)guaranteed?([^a-z]|$)
* 2176775^0 [a-z][<]!.*[>][a-z]
* 2155985^0 ([^a-z]|^)sales?([^a-z]|$)
* 2114136^0 ([^a-z]|^)shipp(ing|ed)?([^a-z]|$)
* 2067398^0 ([^a-z]|^)subscribe(d|r)?([^a-z]|$)
* 2009818^0 ([^a-z]|^)amaz(ing|ed?|ment)([^a-z]|$)
* 1987624^0 ([^a-z]|^)excit(ing|ed?)([^a-z]|$)
* 1939682^0 ([^a-z]|^)absolutely([^a-z]|$)
* 1893703^0 ([^a-z]|^)reveal(ing|ed)?([^a-z]|$)
* 1859794^0 ([^a-z]|^)satisfaction([^a-z]|$)
* 1843555^0 ([^a-z]|^)incredibl(e|y)([^a-z]|$)
* 1719232^0 ([^a-z]|^)apologize([^a-z]|$)
* 1685899^0 ([^a-z]|^)introduc(e|t(ion|ory))([^a-z]|$)
* 1684561^0 ([^a-z]|^)nationwide([^a-z]|$)
* 1675751^0 ([^a-z]|^)media([^a-z]|$)
* 1661918^0 ([^a-z]|^)profit(a(ble|bly))?([^a-z]|$)
* 1655808^0 ([^a-z]|^)inform(ed)?([^a-z]|$)
* 1644924^0 ([^a-z]|^)membership([^a-z]|$)
* 1636605^0 ([^a-z]|^)secret(ly)?([^a-z]|$)
* 1592008^0 ([^a-z]|^)income([^a-z]|$)
* 1543566^0 ([^a-z]|^)market(ing|ed)([^a-z]|$)
* 1479205^0 ([^a-z]|^)success(ful(ly)?)?([^a-z]|$)
* 1468567^0 ([^a-z]|^)unsolicited([^a-z]|$)
* 1468426^0 ([^a-z]|^)unlimited([^a-z]|$)
* 1444170^0 ([^a-z]|^)inexpensive([^a-z]|$)
* 1409686^0 base64
* 1408312^0 ([^a-z]|^)ultimate([^a-z]|$)
* 1293646^0 ([^a-z]|^)credit(ors?)?([^a-z]|$)
* 1289173^0 ([^a-z]|^)newsletter([^a-z]|$)
* 1283100^0 ([^a-z]|^)opportunity([^a-z]|$)
* 1258696^0 ([^a-z]|^)dealer(ships?)?([^a-z]|$)
* 1255685^0 ([^a-z]|^)immediate(ly)?([^a-z]|$)
* 1135436^0 ([^a-z]|^)invest((or|ment)s?)?([^a-z]|$)
* 1045145^0 ([^a-z]|^)million(aire|s)([^a-z]|$)
{
:0
* 8336151^0
* $${SPAMSCORE}^0
{ SPAMSCORE=-"$=" }
}
The conditionals, (for constructional convenience, the logic was inverted from above,) were chosen such that the instance of a specific word increased the SPAMSCORE by the largest amount, while at the same time, having the smallest chance of a false positive, (e.g., choosing the the largest values of -1,000,000 * ln (Pf / (Pf + Ps)),). The two words "unsubscribe" and "mailings" created significant false positive issues with mailing list administrative traffic, (the kind that is distributed monthly containing "As a reminder, you are subscribed to the ... mailing list",) and were commented out to significantly decrease the false positive incident rate. The limit 12272912 was found empirically-it is the value at which there are no false positives of the script on the e-mail archive; and since there were 4,172 e-mail in the archive, a conservative assumption would be that the next e-mail would be a false positive, or the false positive rate equivalent number in the procmail script would be -1,000,000 * ln (1 / 4172) = 8,336,150.81612; which corresponds to about a 3.5 sigma false positive rate. The evaluation:
All-in-all, searching for word frequency rates, (using Bayesian methods,) in the body of e-mail messages seems to be an inferior strategy for spam detection, compared to analyzing only message header information. However, there was a 2% increase in accuracy when using both message header information and word frequency rates in the body of e-mail messages; but at a cost of about a 50% increase in computational resource requirements. At issue is the rather high entropy of the English language-which is why word incident counting and frequency rates are poor indicators of relevance of a document to a specific criteria. (Note: there were five words, of an adult nature, that were omitted from the script, above, to keep it out of the Internet's search engines-for a complete script, contact john@email.johncon.com.) AddendumNote that base64 encoded e-mail message bodies have to be decoded for Bayesian methods. However, such hiding of text is used most frequently in UCE. 37121 non-spam e-mail were placed in a directory, and 3830 recent spam messages in another. Both directories were searched, using a short egrep(1) script with [^a-z]base64[^a-z] as the search argument, and it was found that 700 (700 / 3830 = 0.182767642,) of the spam messages contained the "base64" keyword, vs, 548 (548 / 37488 = 1.46180111E-2,) for the e-mail directory. The value for 1 - Pt, (from the Theory section,) would be 1.46180111E-2 / (1.46180111E-2 + 0.182767642) = 7.40581304E-2. And converting to a procmail conditional value, -1,000,000 * ln (7.40581304E-2) = 2,602,904.94874, or the procmail conditional would look like:
* -2602905^0 [^a-z]base64[^a-z]
So, the data in TABLE VII:
could be included in TABLE I, also, and would preclude having to decode the base64 encoded body of the message. Note, also, that if the header exists:
* -2602905^0 ^content-transfer-encoding:[ ]+base64
that the body would not have to be searched, either. However, of the 3830 spam e-mail messages, 696 had the "Content-Transfer-Encoding: " in the header of the message, and only 2 out of 37488 non-spam messages, so the the spam score could be increased to -1,000,000 * ln (5.33504055E-5 / (5.33504055E-5 + 0.181723238)) = 8,133,652.09579, or:
* -8133652^0 ^content-transfer-encoding:[ ]+base64
ThanksA special note of appreciation to Stephen R. van den Berg, (AKA BuGless,) the author of procmail, who for nine years developed and supported the procmail program, (the "e-mail system administrator's crescent wrench,") for the Internet community. The weighted scoring conditions used in this implementation of UCE filters was added to procmail by van den Berg in June of 1994 with the release of version 3.0, and has successfully been used to filter UCE since that time, (portions of the above script date back to late 1994.) Some Procmail and E-mail "Received: " Header IP Address Auditing How To/Cookbook Examples
LicenseA license is hereby granted to reproduce this software for personal, non-commercial use. THIS PROGRAM IS PROVIDED "AS IS". THE AUTHOR PROVIDES NO WARRANTIES WHATSOEVER, EXPRESSED OR IMPLIED, INCLUDING WARRANTIES OF MERCHANTABILITY, TITLE, OR FITNESS FOR ANY PARTICULAR PURPOSE. THE AUTHOR DOES NOT WARRANT THAT USE OF THIS PROGRAM DOES NOT INFRINGE THE INTELLECTUAL PROPERTY RIGHTS OF ANY THIRD PARTY IN ANY COUNTRY. So there. Copyright © 1992-2005, John Conover, All Rights Reserved. Comments and/or problem reports should be addressed to:
|
Home | John | Connie | Publications | Software | Correspondence | NtropiX | NdustriX | NformatiX | NdeX | Thanks