From: John Conover <john@email.johncon.com>
Subject: logistic non-linear extensions used in tsinvest
Date: 10 Nov 1999 05:32:13 -0000
On the home page of the tsinvest program, http://www.johncon.com/ntropix/,
concerning the tsinvest and tsinvestsim programs, it is mentioned:
"The programs use non-linear extensions to the random walk fractal
model of equity prices. The extensions are similar to the discreet
time "logistic" (parabolic) function. A derivation of the model is
contained in the tsinvest
documentation."
To elaborate on the non-linear extensions, the program tsinvestsim was
used to generate a time series for the tsinvest program using the data
file "tsinvest/tests/optimal.equal.data" from the tsinvest regression
test suite in the source tree, (which represents "typical" data for
stocks on the US equity markets.)
The -j option was used on tsinvest, (which means to use the
non-default method of computing the index of all stocks in the
simulation-similar to the method the equity exchanges use to calculate
the broad market indices,) and the index of the 300 stocks, (all
identical, with a Shannon probability, P, ie., a likelihood of an
increase, of 0.51, optimal growth, ie., a root mean square of the
marginal returns of 0.02,) specified in the data file analyzed. The
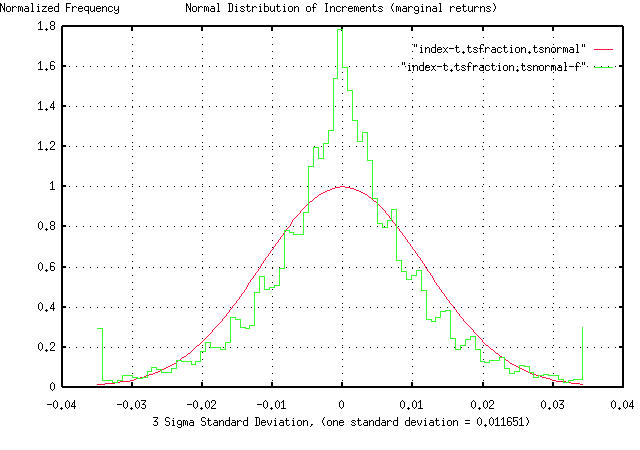
frequency distribution of the marginal returns for the simulated index
is:

and agrees favorably with the frequency distribution of the marginal
returns for the indices of the US equity markets presented at:
http://www.johncon.com/john/correspondence/981229233103.31169.html
Of interest is the kurtosis in both graphs. (Note that in the
simulation, the kurtosis was not the result of persistence, ie., a
Hurst exponent greater than 0.5-it is the result of the non-linearity
of the algorithm used by tsinvestsim, which used a random number
generator, with independent increments, to make the index's increments
a binomial distribution as an approximation to a Gaussian/normal
distribution.)
The Hurst exponent for the simulated index is:
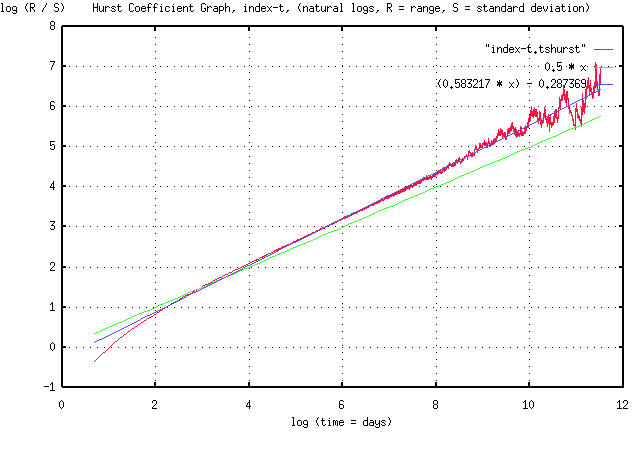
and, also agrees favorably with the Hurst exponent for the NYSE
Composite index presented at:
http://www.johncon.com/john/correspondence/980807151309.11811.html
Likewise, of interest is that the Hurst exponent is greater than
0.5. (Note that in the simulation, the Hurst exponent was not the
result of persistence, it is the result of the non-linearity of the
algorithm used by tsinvestsim, which used a random number generator,
with independent increments, to make the index's increments a binomial
distribution as an approximation to a Gaussian/normal distribution.)
John
--
John Conover, john@email.johncon.com, http://www.johncon.com/